Table of Contents
Properties of Integer Exponents
The properties of integer exponents arise from the basic rules of multiplication and division. They help us simplify and understand expressions involving repeated multiplication. For instance, multiplying two numbers with the same base adds their exponents because you are essentially combining the repeated multiplications. Dividing two numbers with the same base subtracts the exponents, as you are canceling out repeated factors. Raising a power to another power multiplies the exponents because you are repeating the multiplication process multiple times. These properties also explain why any number to the zero power is one, as dividing a number by itself leaves you with one, and why a negative exponent represents a reciprocal, as it indicates division rather than multiplication.

Videos about the properties of exponents:
Exponent properties with products
Exponent properties with parenthesis
Exponent properties with quotients
What is a rational exponent?
Exponentiation is repeated multiplication. For example,
\[5^{2} = 5 \cdot 5
\\\text{ }\\
5^{3} = 5 \cdot 5 \cdot 5
\\\text{ }\\
5^{4} = 5 \cdot 5 \cdot 5 \cdot 5
\\\text{ }\\
\text{etc…}
\]
This makes sense when the exponent is an integer. But what if we allow the exponent to be any rational number? For example,
\[5^\frac{1}{2} = \text{?}
\]
It is not possible to multiply 5 by itself ½ times. So what does this mean? Whatever it means, it must obey the same rules of exponents for integers. For example, it must obey the Power of a Power Property.
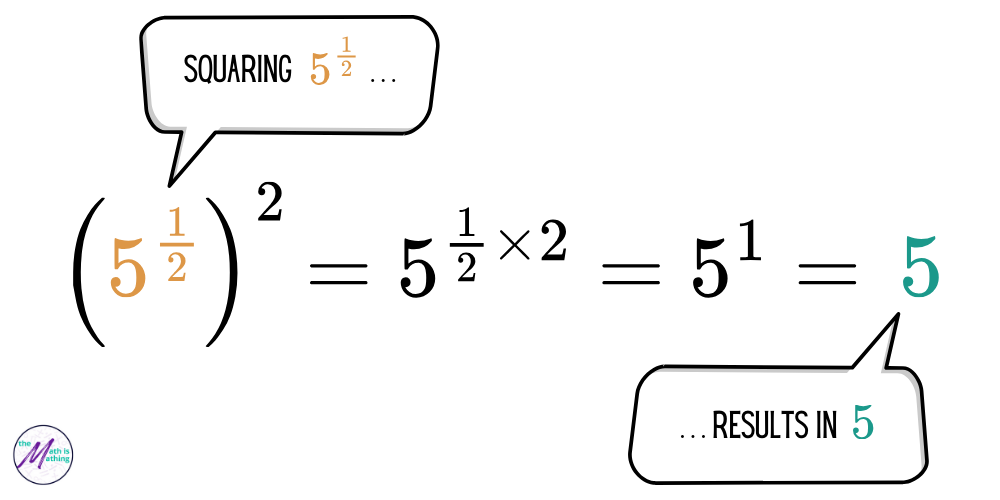
Squaring 5½ result in 5! We already know that a number whose square is 5 is √5, so this means 5½ = √5.
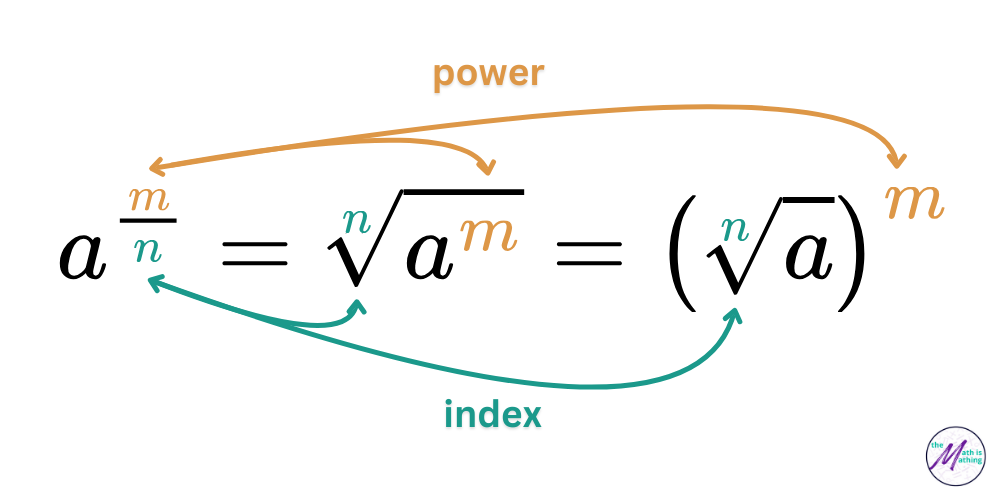
This same definition applies to any rational exponents. If the nth root of a is a real number, and m is an integer, a rational exponent can be rewritten using radicals as follows:
Videos about rational exponents:
What are rational exponents?
Basic fractional exponents
Rewriting roots as rational exponents
Properties of Rational Exponents
As was noted previously, the properties of rational exponents are the same as the properties of integer exponents.

Solving Equations using the Properties of Exponents
We can use the properties of integer and rational exponents to rewrite equations and make them much easier to solve.
Example 1:
Say we are given the following equation and asked to solve for \(x\):
\[ (4^{x+1})(2^{3x-7}) = 2^{25} \]
In order to simplify this process, we can rewrite the bases to all be the same.
\[
\begin{align*}
((2^2)^{x+1})(2^{3x-7}) &= 2^{25} \\
(2^{2(x+1)})(2^{3x-7}) &= 2^{25} \\
(2^{2x+2})(2^{3x-7}) &= 2^{25}
\end{align*}
\]
Now that all the bases are the same, we can apply more of the properties of exponents to rewrite the equation. Here we will use the Product of Powers property.
\[
\begin{align*}
(2x+2)+(3x-7) &= 25 \\
2x+3x+2-7 &= 25 \\
5x – 5 &= 25 \\
5x &= 30 \\
x &= 6
\end{align*}
\]
Example 2:
Say we are asked to solve for \(x\) in the following equation:
\[ 2 = (23^{\frac{1}{6}})(x^{\frac{1}{6}}) \]
We can use the Power of a Product property to multiply the bases on the right side of the equation and keep the exponent.
\[ 2 = (23x)^{\frac{1}{6}} \]
To remove the exponent from the right side of the equation, raise both sides to the power of 6 and simplify.
\[
\begin{align*}
2^6 &= [(23x)^{\frac{1}{6}}]^6 \\
64 &= 23x \\
x &= \frac{64}{23}
\end{align*}
\]

Pingback: Interpreting Exponential Models - The Math is Mathing