Table of Contents
What is a polynomial?
A polynomial is a type of expression in mathematics. The word comes from two different roots: poly, meaning “many” in Greek, and nomen, meaning “name” (or what we refer to as a “term”) in Latin.
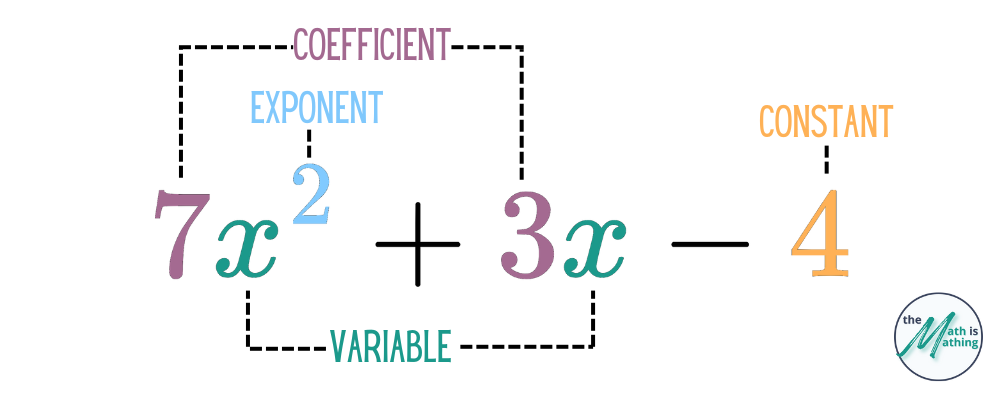
The terms in a polynomial are made up of constants, variables, and exponents (which may only be whole numbers). These elements are combined through addition, subtraction, multiplication, and division (excluding dividing by a variable). Another way to describe this is that polynomials are the sums of terms of the form \(k \cdot x^n\), where \(k\) is any number and \(n\) is a positive integer.
Standard Form of a Polynomial
A polynomial in standard form is a polynomial that is written such that the terms are written in descending order according to their power, or degree.
| NOT Standard Form | Standard Form |
|---|---|
| \[12x^2+5x^3-4+7x\] | \[5x^3+12x^2+7x-4\] |
| \[2x^3+4x^4y^2-5xy\] | \[4x^4y^2+2x^3+-5xy\] |
| \[3a+4-7a^2\] | \[-7a^2+3a+4\] |
| \[8x-5-x^3+7x^4-3x^2\] | \[7x^4-x^3-3x^2+8x-5\] |
Polynomial Names
Polynomials are named by their degree and by the number of terms they are made of.
| Degree | Name |
|---|---|
| 0 degree | constant |
| 1st degree | linear |
| 2nd degree | quadratic |
| 3rd degree | cubic |
| 4th degree | quartic |
| 5th degree | quintic |
| 6th degree | sixth degree |
| Number of Terms | Name |
|---|---|
| 1 | monomial |
| 2 | binomial |
| 3 | trinomial |
| 4 | polynomial of 4 terms |
| 5 | polynomial of 5 terms |
Examples of names of polynomials:
Notice as you review the following table that not all of the polynomials are in standard form. Having the polynomial in standard form makes it easier to name and easier to do mathematical operations on; however, even if it is not in standard form, it is still a polynomial.
| Example | Name |
|---|---|
| \[12x^2+4\] | quadratic binomial |
| \[3m+7m^4-3m^3\] | quartic trinomial |
| \[5y\] | linear monomial |
| \[7\] | constant monomial (or just “constant”) |
| \[9x^5+4\] | quintic binomial |
| \[6x-5x^2-x^3+x^4\] | quartic polynomial of 4 terms |
| \[15+6y^3+y^2-6y\] | cubic polynomial of 4 terms |
| \[8m^2-4m+3\] | quadratic trinomial |
| \[2x+9\] | linear binomial |
Videos about polynomial basics
Polynomials Intro (Khan Academy)
Adding & Subtracting Polynomial Expressions
Adding and subtracting polynomial expressions is done just like adding and subtracting whole numbers. Consider the expressions \(132+406\) and \((x^2+3x+2)+(4x^2+5)\).
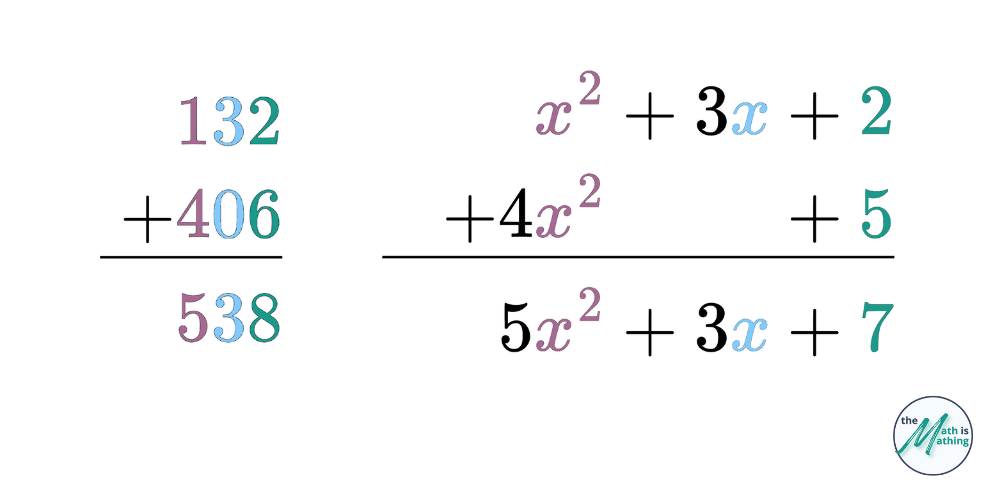
Notice that in just as in the first expression only like place values are added, only like like terms may be added in polynomial expressions.
Examples of Adding and Subtracting Polynomial Expressions
Adding Polynomials
\[
\begin{align*}
(4x^2+5x-2)+(2x^2+7)&=(4x^2 +2x^2) + (5x) + (-2 + 7) \\
&=6x^2+5x+5
\end{align*}
\]
Subtracting Polynomials
\[
\begin{align*}
(4x^2+5x-2)-(2x^2+7)&=(4x^2+5x-2)+(-2x^2-7)\\
&=(4x^2 -2x^2) + (5x) + (-2 – 7)\\
&=2x^2+5x-9
\end{align*}
\]
Videos about adding & subtracting polynomial expressions
Adding Polynomial Expressions
Subtracting Polynomial Expressions
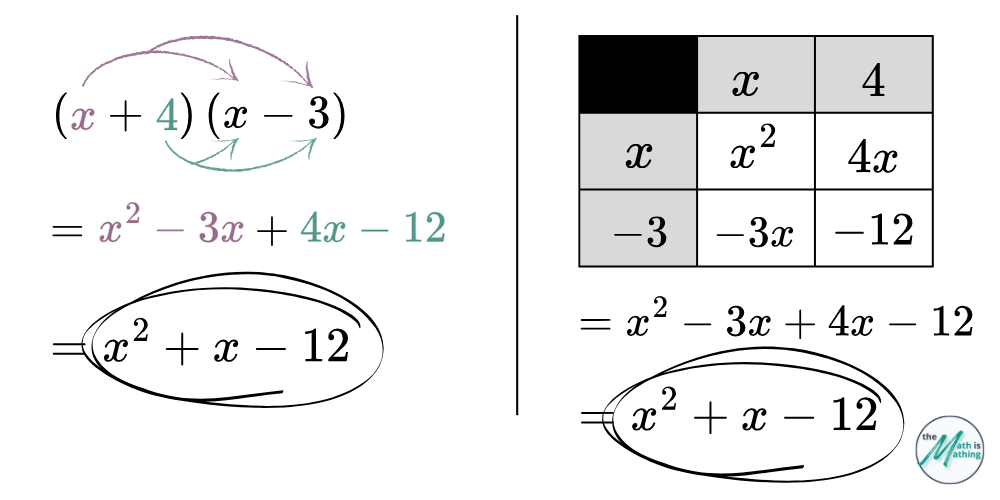
Multiplying Polynomials
There are multiple methods that can be used when multiplying polynomials. Below are two different methods being used to simplify the expression \((x+4)(x-3)\). The method of distribution is shown on the left, using an area model is shown on the right.