Exponential models are important because they help us understand and predict changes over time in various real-world situations, such as calculating interest on savings, modeling population growth, and predicting the spread of diseases. These models show how quantities grow or decay at a constant percentage rate, which is different from linear growth. In finance, they are crucial for understanding how investments grow with compound interest, aiding in financial planning and decision-making. By studying exponential models, you gain valuable tools to analyze and interpret different phenomena, helping you better understand the world and plan for the future.
Table of Contents
General Exponential Model
An exponential function is a type of mathematical function where the input variable is in the exponent (thus the name “exponential”). The general form of an exponential function is \(f(x)=a\cdot b^x\).
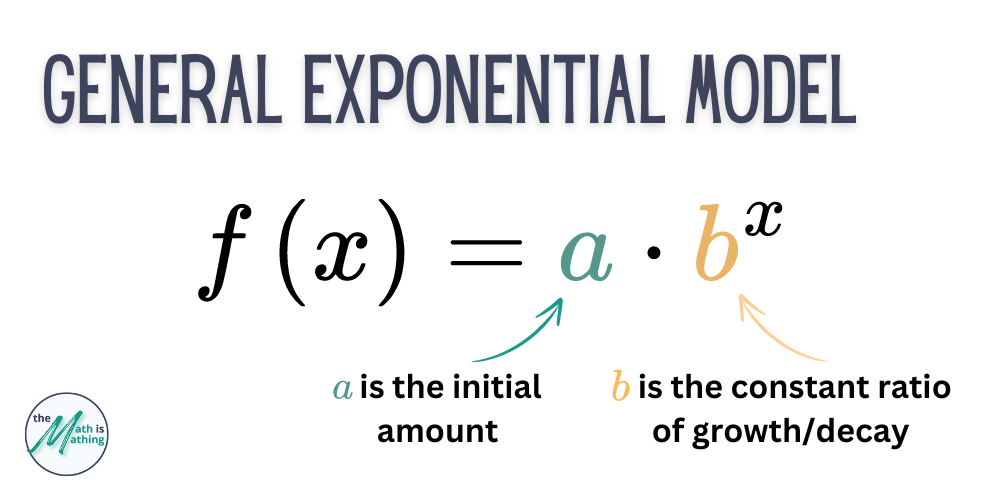
In an exponential function, the value of \(f(x)\) changes rapidly as \(x\) increases or decreases. The constant ratio, \(b\), determines whether the exponential function grows (increases) or decays (decreases) as \(x\) increases.
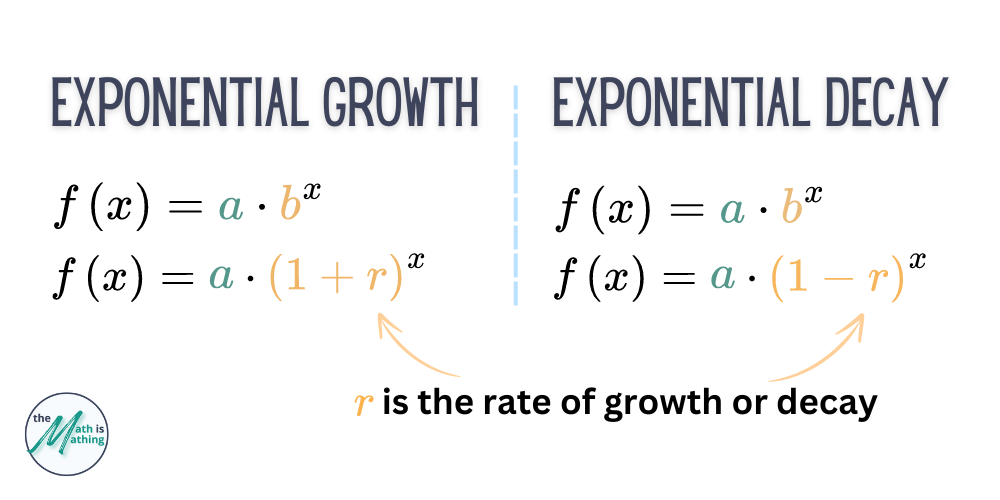
When \(b>1\), the model is of exponential growth. When \(b<1\), the model is of exponential decay.
Videos about exponential growth and decay:
Interpreting Change in Exponential Models
Write an Exponential Growth or Decay Function
Exponential Growth and Decay Word Problems and Functions
Compound Interest
Simple interest is calculated only on the original amount of money (the principal) that you invested or borrowed. The principal does not change over time. We can use the general exponential model to calculate simple interest.
Compound interest is calculated on the initial principal and also on the accumulated interest from previous periods. This means that interest is added to the principal, and then the next period’s interest is calculated on the new total.
For example, if you have $100 in a savings account with a 5% annual interest rate compounded annually, after the first year, you earn $5 in interest, making the total $105. In the second year, you earn interest on $105, not just the original $100.

Continuously compounded interest is a way of calculating interest where the interest is added to the principal an infinite number of times in a given time period. This means the interest is constantly being calculated and added to the principal, leading to faster growth of your investment or loan.
In simple terms, continuously compounded interest grows your money faster than standard compound interest because the interest is being added constantly rather than at regular intervals.

Videos about compound interest:
Compound Interest Formula
Continuously Compounded Interest Formula
What is the natural base “e”?
Click here for a video about the natural base exponential function.
Rewriting Exponential Functions
Sometimes we need to know the rate of growth or decay in relation to a different time frame than the model provides. For example, the model may use a yearly growth rate of 12%, but we need to know the monthly growth rate. Though dividing 12% by 12 would get us close to the monthly growth rate, we need to apply rules of rational exponents in order to find the exact monthly growth rate.
Example 1: Yearly Rate to Monthly Rate
Suppose you have the following exponential function representing yearly growth:
\[f(t)=1000\cdot (1.12)^t \]
where \(t\) is in years and the yearly growth rate is \(12\%\). To convert this to a monthly growth rate, do the following:
\[
\begin{align*}
f(t)&=1000\cdot (1.12)^t \\
&=1000\cdot (1.12)^{t \cdot \frac{12}{12}} \\
&=1000\cdot (1.12)^{\frac{12t}{12}} \\
&=1000\cdot (1.12^\frac{1}{12})^{12t} \\
&\approx1000\cdot (1.0094)^{12t}
\end{align*}
\]
So, the monthly growth rate is approximately \(0.94\%\).
Example 2: Monthly Rate to Quarterly Rate
Suppose you have the following exponential function representing monthly growth:
\[g(t)=500 \cdot (1.02)^t \]
where \(t\) is in months and the monthly growth rate is \(2\%\). To convert this to a quarterly growth rate, do the following:
\[
\begin{align*}
g(t)&=500\cdot (1.02)^t \\
&=500\cdot (1.02)^{t \cdot \frac{3}{3}} \\
&=500\cdot (1.02)^{\frac{3t}{3}} \\
&=500\cdot (1.02^3)^{\frac{t}{3}} \\
&\approx500\cdot (1.061)^{\frac{t}{3}}
\end{align*}
\]
So, the quarterly growth rate is approximately \(6.1\%\).
