Table of Contents

The motivation behind this project
One of the first topics we cover at the beginning of my Integrated Secondary Math 2 course is surrounding the closure of basic arithmetic operations on the rational and irrational number sets (HSN-RN.B.3). I’ve been searching for a good applications project for my students surrounding this topic for the past few years, but I’ve never been able to find one that I liked. So, this year, I created one!
I had to really dig to come up with an idea that didn’t feel like a complete stretch as an application. To be honest, part of this stems from the fact that HSN-RN.B.3 is written as what can easily be interpreted as a DOK Level 1 standard:
“Explain why the sum or product of two rational numbers is rational; that the sum of a rational number and an irrational number is irrational; and that the product of a nonzero rational number and an irrational number is irrational.”
CCSS.Math.Content.HSN.RN.B.3
If you’d like some great questions and lessons from other sources that get students thinking at a higher level with this standards, here are a few of my favorites:
- Tasks from Illustrative Mathematics
- The Classifying Rational and Irrational Numbers lesson from Mathematics Assessment Project
- The Evaluating Statements about Rational and Irrational Numbers lesson from Mathematics Assessment Project
I felt like there was still some exploration / application we could do with this, though. Every time I’ve taught this, it’s felt so primarily theoretical for my students, and I wasn’t always happy with their level of understanding.
My idea was sparked by an article I found on Geeks for Geeks. Let’s introduce students to the fields of cryptography and cybersecurity!
I ultimately decided to present the students with the challenge of creating a password generator (or at least with the idea of password generation — we’ll save coding an actually password generator for another day😅).
Project Objectives
I had two main objectives when creating this assignment:
- Give students the opportunity to explore the difference between rational and irrational numbers in an applied context.
- Make obvious the relationships between rational and irrational numbers as mentioned in the Common Core Standard:
- Explain why the sum or product of two rational numbers is rational
- Explain that the sum of a rational number and an irrational number is irrational
- Explain that the product of a nonzero rational number and an irrational number is irrational.
(I have left the sum and product of two irrational numbers in the project for now; I may remove them later, but I plan on using them as a discussion point when we debrief after the assignment. We’ll see how that goes.)
The basic idea and process of the assignment is relatively simple:
- Students begin by reviewing the definitions of rational and irrational.
- Students identify each of 10 numbers as rational or irrational.
- Students perform operations using those numbers, recording the first 20 digits of the results.
- Students then use a provided table of printable ASCII characters to convert each result into a “randomized” password.
- Students then input the password into an online password strength checker.
- Students answer some reflective questions about why certain passwords were more secure (“randomized”) than others.
Project Details
Reviewing the definitions of rational and irrational
A lot of my students come into my class not knowing what rational and irrational numbers are. Technically it’s an 8th grade standard, but we usually have to cover it from square one. We will already have done some instruction and formative assessment surrounding this, but I felt that scaffolding their knowledge with some vocabulary help as we start the project will be beneficial. I decided to do this by having students complete the key parts of the definitions of the two types of numbers using a word bank.

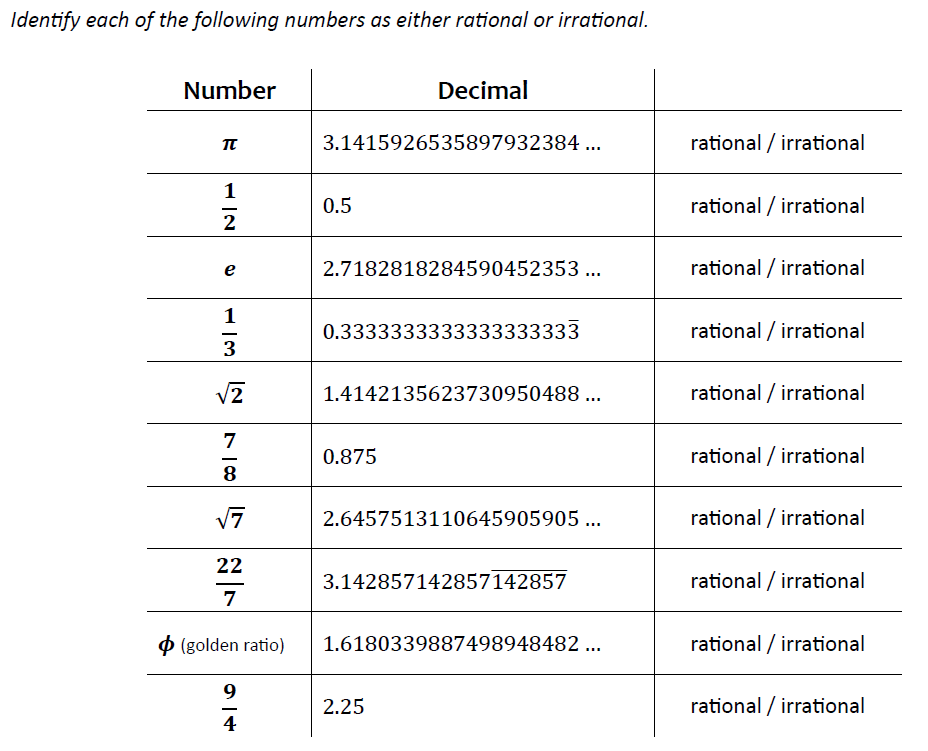
Identify numbers as rational or irrational
Most of the numbers used here have non-terminating decimal equivalents. This was intentional, so as to reduce the number of passwords students create that only have one or two characters. I think that’s an interesting case for students to see and discuss, but I don’t want all of the passwords created from rational results being short. I always wanted to represent the repetitive nature of the decimals of rational numbers with non-terminating decimal equivalents.
Perform operations on rational and irrational numbers
Convert to passwords using an ASCII table
Check password strengths
Reflect
When am I giving my students this project?
This year, I’m going to try running this assignment a day or two after we’ve done our initial investigation of operations on rational and irrational numbers. I don’t think what I’ve developed is robust enough to hold it’s own as the initial investigation of the concept, but it’s got multiple aspects that make it a great way to approach the same thing from another angle.
We’ll already have done a couple days of both theoretical and procedural practice with the concept. I want them to apply it in a completely new way without feeling overwhelmed.
Feedback and Support
I’m looking forward to trying this project out! If you teach this content and have any comments or suggestions regarding this project, feel free to leave them below or email me at mathismathing@gmail.com.
How can I get this project?
If you want to try this project out with your students, head on over to my TPT store to grab it for yourself! If you do want to try it but would like a discount on the product, I’d be happy to give you a discount in exchange for an honest review on the product page on TPT. Just email me to request the discount before buying the product.

